Science – The hat has 13 corners – and solve a puzzle – knowledge

Yorkshire / Bielefeld (dpa) – If you don’t want patterns repeating regularly when laying tiles, you have a team of professional and amateur mathematicians to thank for the new option.

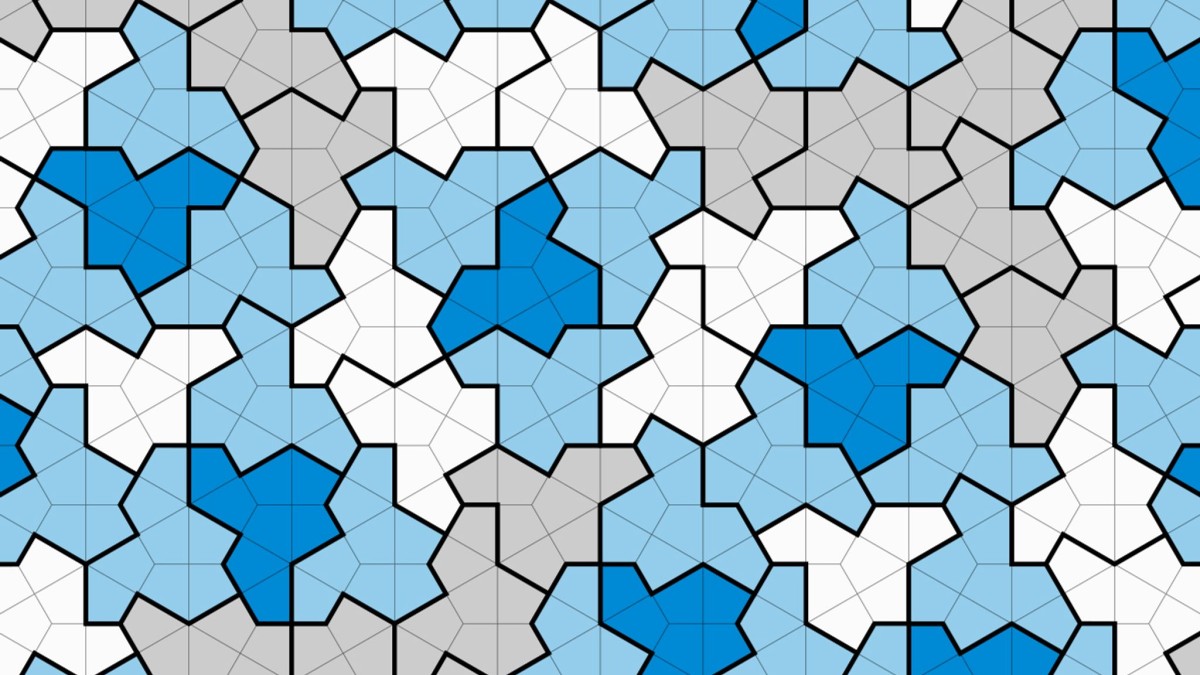
Guys from Great Britain, Canada and the USA have found such a form of tile that it is possible to lay an unlimited surface without gaps, without regularly repeating the basic pattern. Experts call this non-periodic tiling. The tile has 13 corners and, with a little imagination, looks like a hat.

The search for such a model is based on a purely mathematical question, a puzzle — if you will. It has nothing to do with practice. “Non-periodic bishops are rarely used,” says mathematician Dirk Freitloh, who studies this topic at the University of Bielefeld.

A family of non-periodic tile patterns

It’s all down to Roger Penrose and Robert Ammann, who introduced a family of non-periodic tile patterns some 50 years ago—including “Penrose tiles.” However, different shapes of tiles were combined in each case, for example rhombuses with different internal angles. There was a question whether such tiling was also possible with only one tile form. This is called an “Einstein” (“non-periodic monolayer”).

Fritloh explained that all of the previous solutions were not entirely satisfactory. Sometimes it went into three-dimensional space, sometimes the squares overlapped in places, and sometimes there were additional restrictions or rules that seemed artificial.

However, “hat” tiles designed by David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss are not undisputed among connoisseurs. Because with it you can only tile the surface smoothly asymmetrically if you mirror it in several places. Scientists refer to their discovery as “Einstein”. However, critics complain that the tiles don’t cover a gap-free area just by rotating the original shape.

Above all, Frettlöh criticizes the fact that one of the two variables—the original form or the inversion—must always be in the majority. Therefore, all parquet surfaces can be divided into two groups: one with more original tiles, the other with more mirror tiles. With an ideal solution, there is no difference, all conceivable cases are homogeneous.

“You have to look closely.”

In addition, Smith and Co. Any interesting or deep mathematical proof to solve, Fretloh continued. “Even an ordinary person with no mathematical knowledge can solve a lot of mysteries.” The mathematician said that the art of his true specialty does not come on its own. Still, he concedes to the researchers: “It’s now the best example we have.”

Ironically, the offense is not necessarily noticeable when looking at it. “You have to look closely to see the coincidence,” said Tim Roh, a professor of cognitive psychology at the University of Erlangen-Nuremberg. According to him, the fact that the shape of the tiles in the images are always the same helps give the impression that everything looks very regular.

This is because the human brain is always trying to recognize structures – even when none are present. For example, Roh stated that one sometimes thinks one can recognize animals in clouds or faces in slices of bread. “The brain does not work like a camera,” he explained. It receives more or less “noisy signals” and tries to make a model of it.

The perceptual system develops after birth, so only patterns are recognized. For example, there are more vertical and horizontal lines in the environment – which is why people can usually perceive them better than diagonal lines.

© dpa-infocom, dpa: 230427-99-465237/3